Pinocchio Virtual Machine: Nearly Practical Verifiable Computation

At LambdaClass we set up a small research team to work on Zero Knowledge Proofs and Fully Homomorphic Encryption, who in the past few weeks implemented a virtual machine implementing the Pinocchio protocol in Rust.
You can check out the repository at lambdaclass/pinocchio_lambda_vm. It was built by Mauro Toscano, Sergio Chouhy, Agustin Garassino and Diego Kingston.
If you're in need of a team of engineers and researchers who've been working together for a decade in areas like distributed systems, machine learning, compilers, and cryptography, we're your guys. Wanna chat more about it? Book a meeting with us through calendly.
Introduction
zk-SNARKs protocols can be hard to understand for newcomers. One of the first practical implementations is called Pinocchio and it's a very good starting point for anyone trying to get their head around them. Pinocchio's paper can be found here. Having a thorough understanding of its main ideas is of great value to be able to get through the newer and more sofisticated protocols.
In this post we discuss the intuition behind its inner workings and the way it is able to provide succint proofs of circuit executions.
We know that sometimes math seems more complicated and scary than it actually is. And, very often, being able to take a look at some actual code sheds light on what's happening. So we created a companion for this blogpost: a zero-dependency rust implementation of Pinocchio for learning purposes. You can find it at lambdaclass/pinocchio_lambda_vm. We encourage you to go there if you are searching for details not covered here.
So, let's get started!
The problem to solve
The problem that this is trying to solve is the following: someone runs some code with a number of input values. She gets the final result of the program and wants to convince others that this value is actually the output of the execution of that program for the given inputs.
The starting point of this is a process where the program of interest is translated to "arithmetic circuits". In the context of Pinocchio these are directed graphs where the nodes represent arithmetic operations. We'll see now with an example.
By the way, we are not discussing here how to convert the programs to circuits. Our context is the following: someone called a "prover" wants to convince others, the "verifiers", that she executed an arithmetic circuit and got some output values out of it. Let's see what this all means.
Circuit execution
Throughout this post, let's consider a variant of the example circuit from the paper as a running example. The circuit is the following:
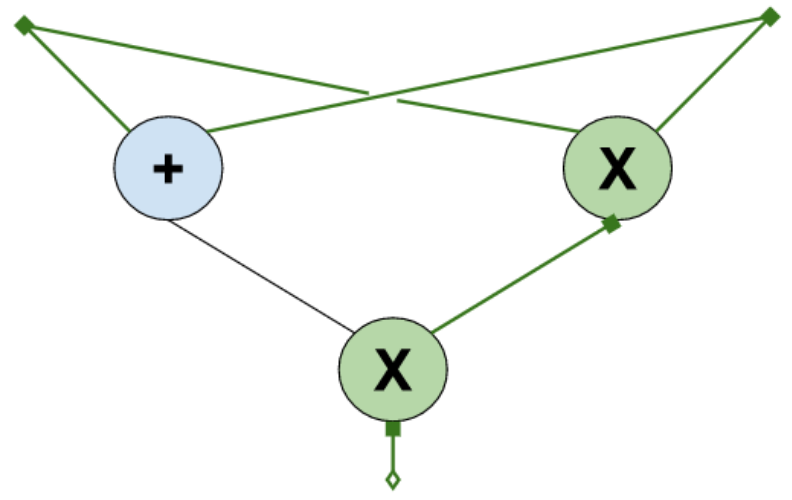
The little squares on the top represent the input values. Choosing input values determines the output values of all the other gates. Executing the circuit means choosing some values for the input gates and filling out the rest of the values corresponding to the output of the multiplication gates. If you are wondering why we are only labeling the output of the multiplication gates, that's normal. The answer is: it's enough to do it this way. We'll come back to this in a moment.
For example, suppose we are working in $\mathbb F_{p}$, for some large prime $p$. The following are two evaluations of the circuit.
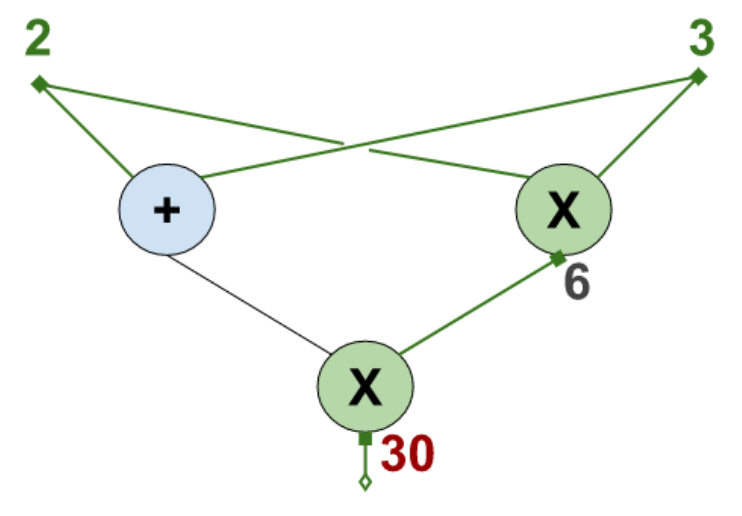
Here the input values are $2$ and $3$. The output is $30$. The unique intermediate value is $6$.
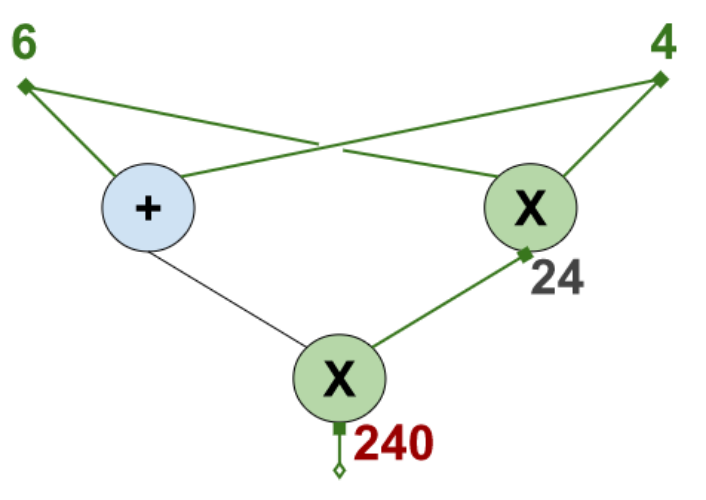
Another evaluation is the following: the input values are $6$ and $4$, the output value is $240$, and the intermediate value is $24$.
Equations that satisfy circuit execution instances
Let's name the input values $c_1, c_2$, the ouput value $c_3$ and the intermediate one $c_4$.
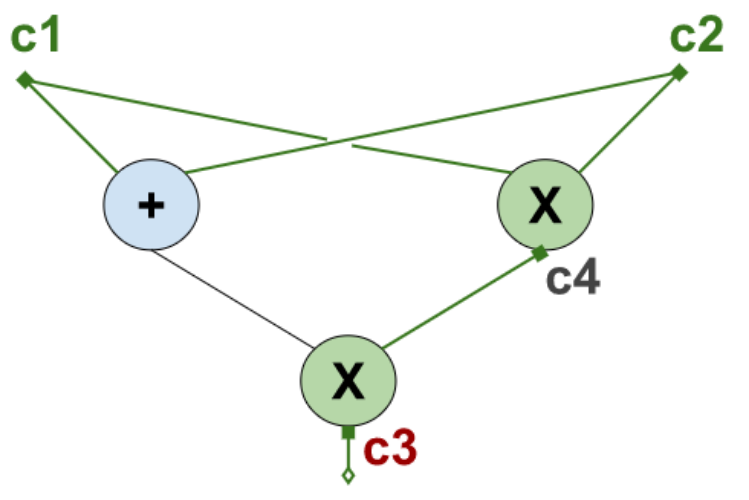
Here is a simple but important observation. It doesn't matter which input values we choose, the resulting values will satisfy the following system of equations:
$c_1c_2 = c_4$
$(c_1+c_2)c_4 = c_3$
Here we have one equation for every multiplication gate. Since we are not labeling the output of the addition gates, we expand them in the left and right operands of the multiplication gate. In this example, that happens only in the left operand of the second equation.
Every set of values $c_1,c_2,c_3,c_4$ that satisfy those two equalities are the values corresponding to an execution instance of the program. They are the unique values corresponding to the execution of the program with input values $c_1$ and $c_2$.
These equations test whether a set of values $c_1,c_2,c_3,c_4$ correspond to an execution instance.
We could have named $c_5$ the output of the addition gate and have the following larger system of equations.
$c_1c_2 = c_4$
$c_1+c_2 = c_5$
$c_5c_4 = c_3$
But it is unnecessary. And not doing so has the advantage that every equation in the resulting system of equations has the form
$$(c_{i_1} + \cdots + c_{i_\alpha})(c_{j_1} + \cdots + c_{j_\beta}) = c_k$$
Note that the second equation in the last system is not of this form. Having all equations of the same shape will be very convenient for the protocol. Moreover, having all the equations of that specific form will be very important, as we'll later see. And we achieve this simply by giving variable names to the input and output values of the multiplication gates, but not addition gates. A system of equations of this form is called a Rank-1 Constraint System (R1CS).
Recap
So, we started from a circuit. By choosing some input values and tracking the output values of every multiplication gate, we obtain a tuple of values $(c_1,\dots,c_N)$ that satisfy a system of equations of a specific form, called R1CS. Moreover, any solution to that system of equations corresponds to some execution of the circuit.
Naive proof of execution
In our example, if we would like to prove that we executed the circuit, we could show the values we got $c_1,c_2,c_3,c_4$. A verifier could then check that the equations hold and be sure that we executed the circuit with input values $c_1$ and $c_2$, and we got $c_3$ as a result. The problem with this is evident: the verification work is the same as executing the circuit. This is useless since we want to delegate heavy computations to untrusted servers and then have concise proof of the execution. So redoing all the work is off the table.
The idea of QAP and Pinocchio is expressing the system of equations in a more compact form as a single polynomial identity. This, together with some fundamental algebra results, will allow us to give a succinct proof of the execution. The amount of work that the verifier will have to do is always the same, regardless of the complexity of the circuit.
Pinocchio's idea of proof of execution
As we will see shortly, there is a very particular and circuit dependant way of constructing a polynomial $p$ out of the values $c_1, c_2, c_3, c_4$ that encodes correct executions. Meaning that $c_1,c_2,c_3,c_4$ are valid execution instance values if and only if their associated polynomial $p$ satisfies a special property. For the circuit of the example, this property is $p$ being equal to $X(X-1)h$ for some polynomial $h$. We'll see shortly where this property comes from. So, the protocol's idea is that the prover constructs the polynomial $p$ and convinces the verifier that there exists $h$ such that $p=X(X-1)h$.
The protocol will be something like this.
- In a setup phase a random point $s$ in $\mathbb F_p$ is chosen and the value $s(s-1)$ is precomputed.
- The prover executes the circuit with public input values $c_1$ and $c_2$ and obtains $c_3,c_4$. She constructs the polynomial $p$ out of these values and computes $h$ such that $p = X(X-1)h$. She evaluates $a = p(s)$ and $b = h(s)$ and sends $a$ and $b$ to the verifier.
- The verifier checks that $a = s(s-1)b$.
We will have to address many disturbing things for this to work. For example:
- How is $p$ constructed?
- Why is it enough to check that $a = s(s-1)b$ to be convinced that $p = X(X-1)h$?
- How does the verifier know that the prover followed the correct recipe to construct $p$ from the values of the circuit's execution?
- How does the verifier know that $a$ and $b$ are values that come from evaluating polynomials $p$ and $h$ at $s$?
- How does the verifier know which public input values were used to execute the circuit?
- What's stopping the prover from simply choosing $b=1$ and $a = s(s-1)$?
- How is this ever going to work?
To address all these questions, the protocol gets more convoluted. But the essence of it is the steps above. The rest comes into play to guarantee that no one is cheating. We'll cover all of these questions, and in the end, we'll obtain the actual Pinocchio protocol.
For more complex circuits, more complex polynomials $p$ are involved, and the condition $p = X(X-1)h$ is replaced with $p = X(X-1)(X-2)\cdots(X-k)h$ for a number $k$ that depends on the number of multiplication gates of the circuit. The idea is still the same. More importantly, the number of checks the verifier has to perform is independent of the circuit!
1. Polynomials to express correct circuit executions
Let's start by showing how we construct the polynomial $p$.
From families of polynomials to systems of equations
Let's forget about our examples and circuits and start by playing around with random polynomials. Let's take $v_1$ as
$$v_1 = X, v_2 = X + 1, v_3 = X + 2$$
$w_1$ as
$$w_1 = 2X + 1, w_2 = 2X + 2, w_3 = 2X + 3$$
and $y_1$ as
$$y_1 = X, y_2 = -X + 1, y_3 = 0$$
Let $c_1,c_2,c_3$ be three elements of $\mathbb F_p$. Out of them, construct the following polynomial
$$p = (c_1v_1 + c_2v_2 + c_3v_3)(c_1w_1 + c_2w_2 + c_3w_3) - (c_1y_1 + c_2y_2 + c_3y_3)$$
We could ask ourselves the following (seemingly unrelated to anything) question: which values $c_1, c_2, c_3$ are such that $p$ has roots at $0$ and $1$? To figure it out, we can evaluate at $0$ and $1$. Precisely, $p(0) = 0$ and $p(1) = 0$ mean
$0 = p(0) = (c_2+2c_3)(c_1 + 2c_2 + 3c_3) - c_2$
$0 = p(1) = (c_1 + 2c_2 + 3c_3)(3c_1 + 4c_2 + 5c_3) - c_3$
$c_1,c_2$, and $c_3$ are such that the polynomial $p$ satisfies $p(0) = 0$ and $p(1) = 0$ if and only if they solve the following system of equations
$(c_2+2c_3)(c_1 + 2c_2 + 3c_3) = c_2$
$(c_1 + 2c_2 + 3c_3)(3c_1 + 4c_2 + 5c_3) = c_3$
On the other hand, the basic theory of polynomials says that $0$ and $1$ are roots of a polynomial $p$ if and only if $X(X-1)$ divides $p$. That is, if and only if there exists a polynomial $h$ such that
$$p = X(X-1)h$$
Takeaway
Wrapping up, we started from sets of polynomials $v_i, w_i, y_i$. These give a way to construct a polynomial $p$ out of any tuple $c_1,c_2,c_3$. The polynomial $p$ is divisible by $X(X-1)$ if and only if the values $c_1,c_2,c_3$ satisfy a system of equations.
This way of encoding systems of equations in a single polynomial identity is the fundamental trick to constructing succinct proofs.
Going back to our circuit
In the previous section, we chose random polynomials. Therefore we got associated with them a system of equations that has nothing to do with our circuit. What we are going to do now is to carefully choose polynomials $v_i, w_i, y_i$, such that the system of equations associated with them is the R1CS of our circuit:
$c_1c_2 = c_4$
$(c_1+c_2)c_4 = c_3$
Since we have four variables $c_1,c_2,c_3$, and $c_4$, we need four polynomials in each family. In other blogposts we will explain how to construct them using polynomial interpolation, but for now, here are the polynomials we want:
$v_1 = 1, v_2 = X, v_3 = 0, v_4 = 0$
$w_1 = 0, w_2 = -X + 1, w_3 = 0, w_4 = X$
$y_1 = 0, y_2 = 0, y_3 = X y_4 = -X + 1$
And for every $(c_1,c_2,c_3,c_4)$ we construct $p$ following this recipe:
$p = (c_1v_1 + c_2v_2 + c_3v_3 + c_4v_4)(c_1w_1 + c_2w_2 + c_3w_3 + c_4w_4) - (c_1y_1 + c_2y_2 + c_3y_3 + c_4y_4)$
$= (c_1 + c_2X)(c_2(-X+1) + c_4X) - (c_3X + c_4(-X + 1))$
We have $p(0) = c_1c_2 - c4$ and $p(1) = (c_1+c_2)c4 - c3$. So $p$ is divisible by $X(X-1)$ if and only if
$c_1c_2 = c_4$
$(c_1+c_2)c_4 = c_3$
Let's plug in some actual values and see what $p$ looks like. Let's start with the tuples of our execution examples. For our first example, we have $(c_1,c_2,c_3,c_4) = (2, 3, 30, 6)$. We get
$p = (2 + 3X)(3(-X+1) + 6X) - (30X + 6(-X+1))$
$ = (2 + 3X)(3X + 3) - (24X + 6)$
$ = 6X + 6 + 9X^2 + 9X - 24X - 6$
$ = 9X^2 -9X$
$ = 9X(X-1)$
For our second example, $(c_1,c_2,c_3,c_4) = (6, 4, 240, 24)$. We obtain
$p = (6 + 4X)(4(-X+1) + 24X) - (240X + 24(-X+1))$
$ = (6 + 4X)(20X + 4) - (216X + 24)$
$ = 120X + 24 + 80X^2 + 16X - 216X - 24$
$ = 80X^2-80X$
$ = 80X(X-1)$
So in both cases $p(0)=0, p(1)=0$, and consequently $p$ is divisible by $X(X-1)$.
Let us see what happens when we choose $(c_1, c_2, c_3, c_4)$ that do not correspond to an execution instance. For example, consider the polynomial $p$ associated with $c_1=1, c_2=1, c_3=0, c_4=0$. These values do not conform to an execution instance of the circuit. We get
$p = (1 + X)((-X+1) + 0X) - (0X + 0(-X+1))$
$= (1 + X)(-X + 1)$
and this polynomial satisfies $p(0) = 1$, so it's not divisible by $X(X-1)$.
Families of polynomials $v_i, w_i, y_i$ that encode circuit execution instances like this exist for any circuit.
Recap
The main goal is to prove the correct execution of a circuit. Showing the values we got $c_1,\dots,c_N$ is not great because the verifier has to do a lot of work to validate them. Polynomials enter here to give an alternative way of showing that information. Out of the values $c_1,\dots,c_N$ we can construct a polynomial $p$. That polynomial has a special property when the values $c_i$ correspond to a valid execution of the circuit. In our example that property is $p$ being divisible by $X(X-1)$. So this gives another way to prove correct executions:
- Show that we properly constructed $p$ following the recipe for the circuit in question.
- Show that $p = X(X-1)h$ for some polynomial $h$.
2. Schwartz-Zippel lemma
A naive way of showing that $p = X(X-1)h$ would be to give the coefficients of $p$ to the verifier and let him divide it by $X(X-1)$ to find that such a polynomial $h$ exists. This isn't good since the amount of work required to do that division scales with the complexity of the circuit. There is a very cheap alternative that appears in every SNARK: show that the equality $p(s) = s(s-1)h(s)$ holds for some random element $s$ in $\mathbb F_p$. The Schwarz-Zippel lemma states that this is enough to be convinced that $p = X(X-1)h$ with high probability. Let's see why.
The key concept here is that of a root of a polynomial. A root of a polynomial $f$ is an element $r \in \mathbb F_p$ such that $f(r)=0$. A fundamental algebra theorem states that a non-zero polynomial of degree $d$ can have, at most, $d$ roots. For example, the polynomial $f = X^5 -3X + 8$ has at most $5$ roots. So if $\mathbb F_p$ has a vast number of elements and we choose a random $s$ in it, the chance of it being one of the $5$ roots of that polynomial is meager. On the other hand, the polynomial $f=0$ is the only one that satisfies $f(s)=0$ for all $s$.
Putting this all together, if $f$ is a polynomial and $f(s)=0$ for a random $s$, then with high probability, we can be sure that $f=0$.
In our case, we have $p$ and $h$ and want to convince a verifier that $p = X(X-1)h$. In other words, we have the polynomial $f = p - X(X-1)h$ and we want to convince the verifier that $f=0$. So using this approach, it's enough to show that $0 = f(s) = p(s) - s(s-1)h(s)$ for a random $s$. This is the same as showing that $p(s) = s(s-1)h(s)$ for a random $s$.
3. Hidings
So far things look a bit silly because we are working with raw elements in $\mathbb F_p$. If the prover sends the verifier $p(s)$ and $h(s)$, she sends two elements of $\mathbb F_p$. So the verifier receives two elements $a, b$ in $\mathbb F_p$ and has no idea how they were produced. Are they random? Are they actually $p(s)$ and $h(s)$? There's no way to tell.
The solution is to work with obfuscated data that allows parties to do a minimal set of operations. The way to obfuscate is pretty simple. We will have a group $G$ and a way to associate to every element of $\mathbb F_p$ its element in $G$ in a way that's hard to invert.
$$\mathbb F_p \longrightarrow G$$
Example
Let's give an example. The number $113$ is prime, and here is a fact we'll use: in $\mathbb Z_{454}$ the element $3$ has the property that $3^{x} \equiv 1$ modulo $454$ if and only if $n \equiv 0$ modulo $113$. This implies that $3^i \equiv 3^j$ modulo $454$ if and only if $i \equiv j$ modulo $113$.
So, we have a field $\mathbb F_{113}$, a group $G=\mathbb Z_{454}$ and the element $3\in\mathbb Z_{454}$. We can use all of this to hide elements of $\mathbb F_{113}$ in $\mathbb Z_{454}$ as follows: the hiding of an element $x\in\mathbb F_{113}$ is $3^x$ modulo $454$.
$\mathbb F_{113} \longrightarrow \mathbb Z_{454}$
$x \mapsto 3^x$
Here are some examples:
$1 \mapsto 3$
$9 \mapsto 161$
$10 \mapsto 29$
$90 \mapsto 65$
Suppose someone chooses a random $s \in \mathbb F_{113}$, computes $3^s$ modulo $454$, and publishes the result. Say the result is $225$. So we know that $3^s \equiv 225$ modulo $454$. It's tough to find out what $s$ is without going through all the possibilities. The brute force attack works here because numbers are small. For larger fields and groups, this becomes infeasible. Assume that's the case for this toy example too. Say there's no way for us to obtain the value of $s$.
Now, even though we don't know $s$, we can compute other hidings off the hiding $3^s$. For example, we know that $3^s = 225$, so
$3^{10s} = 225^{10} = 343$
So, even if we only know the hiding of $s$, we can compute the hiding of $10s$. Moreover we can compute the hiding of $as + b$ for any $a,b$ in $\mathbb F_{113}$: $3^{as+b} = 3^{s a \cdot3^b} = 225^{a \cdot3^b}$. For example
$s \mapsto 225$
$10s \mapsto 343$
$3s+2 \mapsto 155$
In general
The actual group $G$ where hidings live is not that important now. The example above should give a feel of what they look like. But, from now on, we'll assume we have a way to compute hidings. And we'll denote the hiding of an element $x\in\mathbb F_p$ by $E(x)$. In the examples $E(s) = 225$, $E(10s) = 343$.
Checking equations on hidings
We just saw that if we have the hiding $E(s)$ of an unknown element $s$, we can compute the hiding of $as+b$ for any $a$ and $b$. More generally if we have hidings $E(s)$ and $E(t)$, we can compute the hiding of $as + bt$ as
$$E(as+bt) = E(s)^a E(t)^b.$$
This is because we have $E(s)$, $E(t)$, and the rest involves group operations with those two elements. What we can't do is compute $E(st)$, the hiding of $st$, without knowing the raw values $s$ and $t$.
That's sad, but it's not the end of the world. We can get away with it without that. We will need an algorithm that helps us check relations on the original values when we have only their hidings. Precisely, we'll need an algorithm $\mathcal A$ that takes $5$ hidings $E(a), E(b), E(c), E(t), E(d)$ and outputs $1$ if $ab - c = td$, and outputs $0$ otherwise. And the beauty of it is that it won't reveal what the raw values $a,b,c,t,d$ are.
The actual algorithm $\mathcal A$ is something we need to sweep under the rug. The important thing is that such algorithms exist for some groups $G$, especially for elliptic curves. We suggest leaving this as a black box for now.
Note that $\mathcal A(E(a), E(b), E(c), E(0), E(0))$ outputs $1$ if and only if $ab=c$. This will also be useful! Since we'll use this version a lot, we'll call it the algorithm $\mathcal B$. So $\mathcal B$ takes $3$ hidings $E(a)$, $E(b)$ and $E(c)$ and outputs 1 if and only if $c = ab$.
For example, using the hidings from the previous section,
$$\mathcal B(161, 29, 65) = 1.$$
Ok, but why?
Recall that the formula to construct $p$ from values $c_1,c_2,c_3,c_4$ is
$$p = vw - y,$$
where $v = c_1v_1 + c_2v_2 + c_3v_3 + c_4v_4$, $w = c_1w_1 + c_2w_2 + c_3w_3 + c_4w_4$ and $y=c_1y_1 + c_2y_2 + c_3y_3 + c_4y_4$. And if the prover did everything right, she'll be able to find a polynomial $h$ such that $p = X(X-1)h$.
So the idea is that the prover sends $E(v(s))$, $E(w(s))$, $E(y(s))$ and $E(h(s))$ for some unknown value $s$. Then the verifier, who is going to have $E(s(s-1))$, can use algorithm $\mathcal A$ to check that $v(s)w(s) - y(s) = s(s-1)h(s)$. This is exactly $p(s) = s(s-1)h(s)$, the thing we wanted.
Sending the hidings of $v(s)$, $w(s)$, and $y(s)$ instead of the hiding of $p(s)$ has the advantage that recipes for constructing $v, w$ and $y$ are way much easier than the recipe to build $p$. They are linear combinations of the base polynomials $v_i, w_i, y_i$. And, as we'll see now, there's a way to prove we correctly constructed those polynomials in the land of hidings.
Recap
Instead of raw values, the prover and verifier will have to work with hidings. The setup phase will produce enough hidings so the prover can compute the values it needs to show to the verifier. And that will be enough for him to be convinced that the prover properly executed the circuit. And with some tricks, we can guarantee that the prover can't cheat.
4. Intuition on how to prove correct constructions of polynomials
Let's start addressing the third question: how does the verifier know that the prover followed the correct recipe to construct a polynomial?
What follows is an intuition on how the protocol solves this issue. Why do we say it is an intuition? Well, it has gaps. We'll discuss the actual security proofs in other blogposts.
See for yourself if you can spot the gaps!
Proving correct construction of $v$
Let's start with $v$. What we want is to somehow send $E(v(s))$ to the verifier along with some redundant information that proves that $v(s) = c_1v_1(s) + c_2v_2(s) + c_3v_3(s) + c_4v_4(s)$. But without giving away the values $c_1,c_2,c_3,c_4$.
Let's go back to our example. We have $v_1,v_2,v_3,v_4$. And assume there was a setup phase in which random $s$ and $\alpha$ were sampled from $\mathbb F_p$, and the following evaluation and verification keys were publicly published
Evaluation key:
$E(v_1(s)), E(v_2(s)), E(v_3(s)), E(v_4(s)),$
$E(\alpha v_1(s)), E(\alpha v_2(s)), E(\alpha v_3(s)), E(\alpha v_4(s)).$
Verification Key:
$$E(\alpha)$$
The values $s$ and $\alpha$ are not known to anyone and were discarded. Suppose the prover has already executed the circuit, obtained $c_1,c_2,c_3,c_4$, and constructed $v$. She wants to send the verifier $v(s)$, but she doesn't know $s$. She can then use the evaluation key to send its hiding: $E(v(s))$. So the prover constructs the following elements and sends them to the verifier:
$E(v(s)) = E(v_1(s))^{c_1} E(v_2(s))^{c_2} E(v_3(s))^{c_3} E(v_4(s))^{c_4} ,$
$E(\alpha v(s)) = E(\alpha v_1(s))^{c_1}E(\alpha v_2(s))^{c_2}E(\alpha v_3(s))^{c_3}E(\alpha v_4(s))^{c_4}.$
Note that the right-hand sides depend on elements known to the prover.
The verifier receives these two elements. Let's call them $V=E(v(s))$ and $V'=E(\alpha v(s))$. But the verifier doesn't trust the prover, so for the moment, he knows that he received two hidings $V=E(x)$ and $V'=E(y)$ of some elements $x$ and $y$. And he wants to be convinced that $x = c_1v_1(s) + c_2v_2(s) + c_3v_3(s) + c_4v_4(s)$ for some $c_1,c_2,c_3,c_4$. If those values correspond to a correct evaluation of the circuit is something we are not worrying about right now, and another check will cover that. What we are doing right now is just checking that $x$ is an evaluation at $s$ of a polynomial constructed in a very particular way.
The verifier performs the following check using the verification key
$$\text{Check that }\mathcal B(V, E(\alpha), V')\text{ equals }1$$
If the prover did everything right, the check would pass. From the verifier's end, if the check passes, let's see what he can be sure about. If the check passes, since $V=E(x)$ and $V'=E(y)$, he knows that $y=\alpha x$. Looking at the evaluation key, he sees that the prover doesn't know the raw value of $\alpha$. The only thing the prover knows related to $\alpha$ is the hidings $E(\alpha v_i(s))$ in the evaluation key. So the only way the prover could have ever constructed the hiding of a multiple of $\alpha$ is from the values $E(\alpha v_i(s))$. And the only thing that can be constructed using them and the group operation is
$E(\alpha v_1(s))^{c_1}E(\alpha v_2(s))^{c_2}E(\alpha v_3(s))^{c_3}E(\alpha v_4(s))^{c_4} = E(c_1\alpha v_1(s) + c_2\alpha v_2(s) + c_3\alpha v_3(s) + c_4\alpha v_4(s)))$
$= E(\alpha(c_1v_1(s) + c_2v_2(s) + c_3v_3(s) + c_4v_4(s)))$
for some $c_1,c_2,c_3,c_4$. So $V'=E(\alpha x)$ has to be of the form above. This implies that $\alpha x = \alpha(c_1v_1(s) + c_2v_2(s) + c_3v_3(s) + c_4v_4(s))$, and therefore the verifier is in possession of
$$V = E(x) = E(c_1v_1(s) + c_2v_2(s) + c_3v_3(s) + c_4v_4(s)).$$
And that's how the verifier gets convinced that the prover sent him $V=E(v(s))$ where $v$ is a polynomial constructed using the correct recipe!
A gap
Did you spot it? The problem lies in the phrase, "The only thing the prover knows related to $\alpha$ are the hidings $E(\alpha v_i(s))$ in the evaluation key." That's false because the verification key is also public and potentially known to the prover. The prover also has $E(\alpha)$. She could use it. For example, she could choose any $z$ and send the verifier $V=E(z)$ and $V'=E(\alpha)^z = E(\alpha z)$. And that would pass the verifier's check without being $z = v(s)$ for any linear combination $v$ of the polynomials $v_i$.
To this point, this is what we have and the prover could sneak in that $z$ if she wants. It's unclear how the prover could use that flexibility to construct fake proofs. And she actually can't without breaking some cryptographic assumptions first. But that proof takes another path. For now, let's continue with our intuition ignoring this fact.
Intuition continues
Even though there's this glitch we just discussed, this idea gives an obvious use case of hidings to convince a verifier that a value was produced in a very particular way.
Since the prover needs to send also $E(w(s))$ and $E(y(s))$, there must be a trusted setup publishing enough hidings to construct them. This is what it would look like.
So to send all $E(v(s))$, $E(w(s))$ and $E(y(s))$ we need a trusted setup that samples random $s$, $\alpha_v$, $\alpha_w$, $\alpha_y$ and publishes
- Evaluation key: for all $i$
$E(v_i(s)), E(\alpha_v v_i(s)),$
$E(w_i(s)), E(\alpha_w w_i(s)),$
$E(y_i(s)), E(\alpha_y y_i(s)),$
- Verification Key: $E(\alpha_v), E(\alpha_w), E(\alpha_y)$.
With all this, the prover can construct all the hidings and send them to the verifier. He follows all the checks and gets convinced that he received $E(v(s)))$, $E(w(s))$ and $E(y(s))$, where $v, w$ and $y$ are linear combinations of the respective $v_i, w_i$ and $y_i$.
But there's a problem with that. Let's repeat what we just said in more detail to see it.
The verifier gets convinced that he received $E(v(s))$, where $v(s)$ is some linear combination of the $v_i(s)$, say $v(s) = av_1(s) + bv_2(s) + cv_3(s) + dv_4(s)$ for some values $a,b,c,d$.
On the other hand he also received $E(w(s))$, where $w(s)$ is some linear combination of the elements $w_i(s)$, say $w(s) = a'v_1(s) + b'v_2(s) + c'v_3(s) + d'v_4(s)$ for some values $a',b',c',d'$. And that's the problem. The verifier has no guarantee that $a=a'$, $b=b'$, $c=c'$, and $d=d'$. And that's important! Because $v, w$ and $y$ need to be constructed using the same values $c_1,c_2,c_3,c_4$. That's part of the recipe to construct $p$.
So we need something that connects the three hidings sent by the prover. Because so far, they are independent, and so are the three checks of the verifier.
Proving construction of all $v,w,y$
The solution is to use the same trick cleverly yet again. And things start to get weird.
The setup phase will now sample random $s, \alpha_v, \alpha_w, \alpha_y, \beta$ and publishes the following keys
Evaluation key:
$E(v_i(s)), E(\alpha_v v_i(s)),$
$E(w_i(s)), E(\alpha_w w_i(s)),$
$E(y_i(s)), E(\alpha_y y_i(s)),$
$E(\beta(v_i(s) + w_i(s) + y_i(s))).$
Verification Key:
$$E(\alpha_v), E(\alpha_w), E(\alpha_y), E(\beta)$$
As before the prover obtains $c_1,c_2,c_3,c_4$ and uses the evaluation key to compute $E(v(s))$, $E(\alpha_v v(s))$, $E(w(s))$, $E(\alpha_w w(s))$, $E(y(s))$, $E(\alpha_y y(s))$. But now she can also use the new elements of the evaluation key to compute $E(\beta (v(s) + w(s) + y(s)))$. She sends these seven elements to the verifier. The verifier receives seven hidings. Let's denote them $V,V', W, W', Y, Y', Z$ in the order the prover sent them.
The verifier performs the following checks:
- Check that $\mathcal B(V, E(\alpha_v), V')$, $\mathcal B(W, E(\alpha_w), W')$, and $\mathcal B(Y, E(\alpha_y), Y')$ all equal $1$.
- He computes $VWY$ using the group operation and checks that $\mathcal B(VWY, E(\beta), Z)$ equals $1$
If all these tests pass, the prover will convince the verifier that
$V = E(av_1(s) + bv_1(s) + cv_3(s) + dv_4(s)),$
$W = E(aw_1(s) + bw_2(s) + cw_3(s) + dw_4(s))$
$Y = E(ay_1(s) + by_2(s) + cy_3(s) + dy_4(s))$
for some elements $a,b,c,d$. And the reason is very similar to the previous case. The second check guarantees that $Z$ is the hiding of some multiple of $\beta$. The only way that it could have been produced is using the new hidings $E(\beta(v_i(s) + w_i(s) + y_i(s)))$. With such hidings the prover can only compute $E(\beta(v(s) + w(s) + y(s)))$ where $v,w$ and $y$ are linear combinations of the $v_i$, $y_i$ and $w_i$, respectively, with the same coefficients. That, and again using the second check passed, implies that the coefficients in the raw values of $V, W$, and $Y$ are the same.
What about $h$?
As we said previously, the prover is sending $E(v(s))$, $E(w(s))$ and $E(y(s))$ because the verifier can use them to check that $\mathcal A(E(v), E(w), E(y), E(s(s-1)), E(h(s)))$ equals $1$. For that the verifier needs both $E(s(s-1))$ and $E(h(s))$. The value $E(s(s-1))$ is independent of the particular execution of the circuit and can be added to the verifying key. Concerning $E(h(s))$, the prover needs to provide that. So she needs to be able to construct it. The hidings on the evaluation key are insufficient now since $h$ won't be, in general, any linear combination of the polynomials $v_i, w_i, y_i$. The solution is to add $E(s^i)$ to the evaluation key for as many values $i$ as are needed to construct $h$ in the worst case.
To keep this short, we will wait to add this to the protocol. We'll cover the remaining issue and then write down the final protocol.
Recap
With all this, the prover can construct hidings of $v(s)$, $w(s)$,$y(s), h(s)$ and convince the verifier that she followed the correct recipe to build the polynomials $v,w,y$. And moreover that $p = vw-y=X(X-1)h$. This answers the third and fourth questions of the beginning!
5. Inputs and outputs
Let's answer question 5. How does the verifier know that the prover used the input values $c_1$ and $c_2$? This is very simple. Recall that the verifier expects a proof of execution of the circuit on inputs $c_1,c_2$. So the prover executes the circuit, obtains the output $c_3$, and communicates $c_3$ to the verifier. So the verifier knows $c_1,c_2$, and $c_3$. In general, the verifier knows all public input and output values. Therefore we can modify the protocol slightly to allow the verifier to check inputs and outputs.
The polynomial $p$ is equal to $vw - y$ where $v = c_1v_1 + c_2v_2 + c_3v_3 + c_4v_4$ and similarly for $w$ and $y$. And the verifier is expecting to receive, for instance, the hiding $E(v(s))$ as part of the proof. But the input/output part of $E(v(s))$ is something the verifier can compute by himself. More precisely, he knows $c_1,c_2,c_3$ and $E(v_1(s))$, $E(v_2(s))$ and $E(v_3(s))$ since they are part of the public evaluation key so far. So he can compute
$$E(c_1v_1(s) + c_1v_2(s) + c_3v_3(s)) = E(v_1(s))^{c_1} E(v_2(s))^{c_2} E(v_3(s))^{c_3}$$
This means that if the prover only sends him $V = E(c_4v_4(s))$, then the verifier can complete it with the above to obtain $E(v(s))$:
$$E(v(s)) = E(c_1v_1(s) + c_1v_2(s) + c_3v_3(s))V$$
And doing so, he gets the guarantee that the terms in $v(s)$ corresponding to the input/output are the ones he expects.
Note that if we do this, the prover won't need the hidings $E(v_1(s))$, $E(v_2)$, and $E(v_3(s))$ anymore. So we are moving them to the verifying key.
Let's write down what we have so far!
6. Final protocol
Almost the final protocol for the example
Recall that we assume there is a hiding function $E: \mathbb F_p \to G$ for some group $G$ and that there exists an algorithm $\mathcal A$ such that $\mathcal A(E(a), E(b), E(c), E(t), E(h)) = 1$ if and only if $ab-c=th$. We define $\mathcal B(E(a), E(b), E(c)) := \mathcal A(E(a), E(b), E(c), E(0), E(0))$ which outputs $1$ if and only if $ab=c$. Also recall that $E(a)E(b) = E(a+b)$.
1. Setup
Five random elements $s, \alpha_v, \alpha_w, \alpha_y, \beta$ are sampled from $\mathbb F_p$. Two public keys are generated from them: the evaluation key and the verification key
3.1 Evaluation Key:
$E(v_4(s)), E(w_4(s)), E(y_4(s)),$
$E(\alpha_vv_4(s)), E(\alpha_ww_4(s)), E(\alpha_yy_4(s)),$
$E(\beta(v_4(s) + w_4(s) + y_4(s))),$
$E(1)$
3.2 Evaluation Key:
$E(\alpha_v), E(\alpha_w), E(\alpha_y), E(\beta),$
$E(v_1(s)), E(v_2(s)), E(v_3(s)),$
$E(w_1(s)), E(w_2(s)), E(w_3(s)),$
$E(y_1(s)), E(y_2(s)), E(y_3(s)),$
$E(s(s-1))$
2. Proof generation
The prover executes the circuit with public input values $c_1, c_2$, obtains the output value $c_3$, and the intermediate value $c_4$. She computes
$v = c_1v_1 + c_2v_2 + c_3v_3 + c_4v_4$
$w = c_1w_1 + c_2w_2 + c_3w_3 + c_4w_4$
$y = c_1y_1 + c_2y_2 + c_3y_3 + c_4y_4$
$p = vw - y$
She also computes $h$ such that $p = X(X-1)h$. The polynomial $h$ must be of degree $0$ for this particular circuit, so it is a constant value in $\mathbb F_p$.
The prover computes the following hidings from the evaluation key.
$\pi = (E(c_4v_4(s)), E(\alpha_vc_4v_4(s)),$
$E(c_4w_4(s)), E(\alpha_wc_4w_4(s)),$
$E(c_4y_4(s)), E(\alpha_yc_4y_4(s)),$
$E(\beta c_4(v_4(s) + w_4(s) + y_4(s)),$
$E(h))$
The prover sends the output value $c_3$ to the verifier and the proof $\pi$.
3. Verification
The verifier receives the output value $c_3$ and the proof $\pi = (V, V', W, W', Y, Y', Z, H)$. He computes the input/output parts from the verification key.
$V_{IO} = E(c_1v_1(s) + c_2v_2(s) + c_3v_3(s))$
$W_{IO} = E(c_1w_1(s) + c_2w_2(s) + c_3w_3(s))$
$Y_{IO} = E(c_1y_1(s) + c_2y_2(s) + c_3y_3(s))$
He performs the following checks
- $\mathcal B(V', V, E(\alpha_v)) = 1$, $\mathcal B(W', W, E(\alpha_w)) = 1$, $\mathcal B(Y', Y, E(\alpha_y)) = 1$,
- $\mathcal B(VWY, E(\beta), Z)=1$,
- $\mathcal A(V_{IO}V, W_{IO}W, Y_{IO}Y, E(s(s-1)), H) = 1$.
If all checks pass, the verifier gets convinced that the prover executed the circuit with input values $c_1,c_2$ and obtained the output value $c_3$.
Pinocchio's protocol
Now we give the actual protocol for a general circuit. Suppose the circuit has $n_I$ input values and $n_O$ output values.
As before, let $E$ be the hiding function and $\mathcal A$ and $\mathcal B$ the algorithms to check equations on hidings.
Let $N=n_I + n_O$. Executing the circuit with input values $(c_1,\dots,c_{n_I})$ outputs the values $(c_{n_I+1},\dots, c_{N})$ and all the intermediate values $(c_{N+1}, \dots, c_m)$. Putting these tuples together, we say that $(c_1,\dots,c_m)$ are the values of the execution of the circuit.
In the example, we had $n_I=2, n_O=1$, $N=3$ and therefore executing the circuit with input values $(c_1,c_2)$ produces the output value $c_3$ and the intermediate value $c_4$.
Let $d$ be the number of multiplication gates in the circuit. Let $t = X(X-1)(X-2)\cdots (X-d)$. There exist families of polynomials $v_i,w_i,y_i$, with $i=1,\dots, m$, such that $(c_1,\dots,c_m)$ are the values of the execution of the circuit if and only if $p = vw-y$ is divisible by $t$, where $v=\sum_i c_iv_i$, $w=\sum_ic_iw_i$ and $y=\sum_ic_iy_i$.
In our example $t = X(X-1)$.
1. Setup
Eight random elements $s, r_v, r_w, \alpha_v, \alpha_w, \alpha_y, \beta, \gamma$ are sampled from $\mathbb F_p$. Let $r_y=r_vr_w$. Two public keys are generated from them: the evaluation key and the verification key
3.1 Evaluation Key: For all $i=N+1,\dots,m$, and for all $j=1,\dots,d-2$
$E(r_vv_i(s)), E(r_ww_i(s)), E(r_yy_i(s)),$
$E(\alpha_vr_vv_i(s)), E(\alpha_wr_ww_i(s)), E(\alpha_yr_yy_i(s)),$
$E(\beta(r_vv_i(s) + r_ww_i(s) + r_yy_i(s))),$
$E(s^j)$
3.2 Evaluation Key: For all $i=1,\dots, N$
$E(\alpha_v), E(\alpha_w), E(\alpha_y), E(\beta\gamma), E(\gamma)$
$E(r_vv_i(s)),$
$E(r_ww_i(s)),$
$E(r_yy_i(s)),$
$E(t(s))$
2. Proof generation
The prover executes the circuit with input values $(c_1,\dots,c_{n_I})$ and obtains the values $(c_1,\dots,c_m)$. She computes:
$v = \sum_{i=1}^m c_iv_i$
$w = \sum_{i=1}^m c_iw_i$
$y = \sum_{i=1}^m c_iy_i$
$p = vw - y$
She also computes $h$ such that $p = th$. The polynomial $h$ is of degree at most $d$.
The prover computes the following hidings from the evaluation key. Note that all the sums here have $i$ ranging from $N+1$ to $m$. That corresponds to the indices of the intermediate values.
$\pi = (E(\sum_{i=N+1}^mc_ir_vv_i(s)), E(\alpha_v\sum_{i=N+1}^mr_vc_iv_i(s)),$
$E(\sum_{i=N+1}^mc_ir_ww_i(s)), E(\alpha_w\sum_{i=N+1}^mr_wc_iw_i(s)),$
$E(\sum_{i=N+1}^mc_ir_yy_i(s)), E(\alpha_y\sum_{i=N+1}^mr_yc_iy_i(s)),$
$E(\beta \sum_{i=N+1}^mr_vc_iv_i(s) + r_wc_iw_i(s) + r_ic_iy_i(s)),$
$E(h))$
The prover sends the output values $(c_{n_O+1},\dots,c_N)$ to the verifier and the proof $\pi$.
3. Verification
The verifier receives the output values $(c_{n_O},\dots, c_N)$ and the proof $\pi = (V, V', W, W', Y, Y', Z, H)$. He computes the input/output parts from the verification key. Note that all sums here have $i$ ranging from $1$ to $N$. That corresponds to the input/output indices.
$V_{IO} = E(\sum_{i=1}^Nc_ir_vv_i(s))$
$W_{IO} = E(\sum_{i=1}^Nc_ir_ww_i(s))$
$Y_{IO} = E(\sum_{i=1}^Nc_ir_yy_i(s))$
He performs the following checks
- $\mathcal B(V', V, E(\alpha_v)) = 1$, $\mathcal B(W', W, E(\alpha_w)) = 1$, $\mathcal B(Y', Y, E(\alpha_y)) = 1$,
- $\mathcal A(Z, E(\gamma), E(0), VWY, E(\beta\gamma))=1$,
- $\mathcal A(V_{IO}V, W_{IO}W, Y_{IO}Y, E(t(s)), H) = 1$.
- If all checks pass, the verifier gets convinced that the prover executed the circuit with input values $(c_1,\dots,c_{n_I})$ and obtained the output values $(c_{n_O+1}, \dots, c_N)$.