Soss: Probabilistic Programming with Julia

An interview with its creator, Chad Scherrer

By: Javier Rodríguez Chatruc and Federico Carrone

Probabilistic programming is at this point an established field both for research and industry applications, but like everything else (especially in the tech industry), it is undergoing constant evolution. This is where Julia comes in — designed for high performance in the world of data science, it seems to be the perfect fit for probabilistic programming.

To learn more about this world we contacted Chad Scherrer, the creator of Soss, a probabilistic programming library written entirely in Julia. With a very clean syntax resembling math notation, Soss seems to bridge the gap between the more academic side of data science and the more technical/developer one, while also providing speed and first-class models.

Please tell us a bit about yourself. What is your background? what is your current position?

Starting out, I thought I would end up focusing on algebraic topology. So I did coursework along these lines for a few years before switching to stats. My thesis is on a special case of multivariate normal distributions with a group symmetry, so algebra still plays a big part.

After graduating, I worked at Pacific Northwest National Laboratory, mostly doing computational statistics. I learned some Python, then R. The high-level coding was nice, but I was frustrated by how awkward it was to make it fast.

One day I came across this “Great Computer Language Shootout”, where Ocaml was really dominating. So I used that for a few years. Then multicore hardware started really picking up, but at the time the Ocaml team said they wouldn’t really be doing anything with SMP (symmetric multiprocessing). So I started looking around again, and found Haskell.

Along the way, I had collaborated with the high-performance computing group doing parallel machine learning using C/OpenMP. And I started getting interested in probabilistic programming. I wanted to make something like JAGS, but using Haskell and allowing more high-level expressiveness. So I collaborated with Galois to develop Passage, which works in terms of a now-standard probability monad, and produces C/OpenMP code for parallel Gibbs sampling.

Based on the Passage work, Galois started getting involved with Probabilistic Programming for Advancing Machine Learning (PPAML), but they needed someone to serve as technical lead. So I moved to Portland and did that for a few years. Galois is a (mostly) Haskell shop, so I was able to dig deeper into both Haskell and probabilistic programming.

Still wanting to extend some of the ideas from Passage, I moved to Seattle and spent a couple of years at Metis teaching data science. In my free time, I got more up to speed on Julia, and started work on what would become Soss.

These days, I work as a Senior Research Scientist at RelationalAI. Most machine learning pipelines treat database queries and model training as entirely independent, so to go between them requires throwing away all of the structure and just joining everything.

As it turns out, that throws away some big opportunities for optimization. So our system has an expressive language for reasoning about relational structure, and works in terms that make these optimizations natural for machine learning and probabilistic programming.

What is probabilistic programming? How does it differ from other forms of programming?

When people talk about Probabilistic Programming Languages (PPLs), they usually mean a system for building and reasoning about Bayesian models. Maybe the simplest way to think about this is as a way of reasoning about simulations. Say you have a simulation that you can run to make a simulated “world”. Every part of the simulation has some randomness. This includes the things you can actually observe, but also the underlying choices the simulator made for things that affect those observations. But those are random too, so they might depend on other random choices.

Ok, so choices made along the way will affect the distribution of things downstream. But we can also use this to reason the other way! We observe some data, and ask “what choices along the way could have led to this?”

In the simplest case, say we have a simulation for biased coin flips where we pick a random probability of heads, say p ~ Uniform(0,1), and simulate 20 flips. Then we observe 15 heads and 5 tails. We can’t say for certain what p was, but we can find a distribution that’s updated based on the observed data.

How did you get into Julia? Why choose Julia over Python or R?

I want to be able to express ideas at a high level of abstraction without sacrificing performance. I’ve used Python and R quite a bit, for the things I wanted to do I always felt constrained because getting performance always means pushing things to another language. Then there are concerns with the cost of crossing that language barrier, both in a human and computational sense.

What is Soss? How did it come about and what was the motivation behind it?

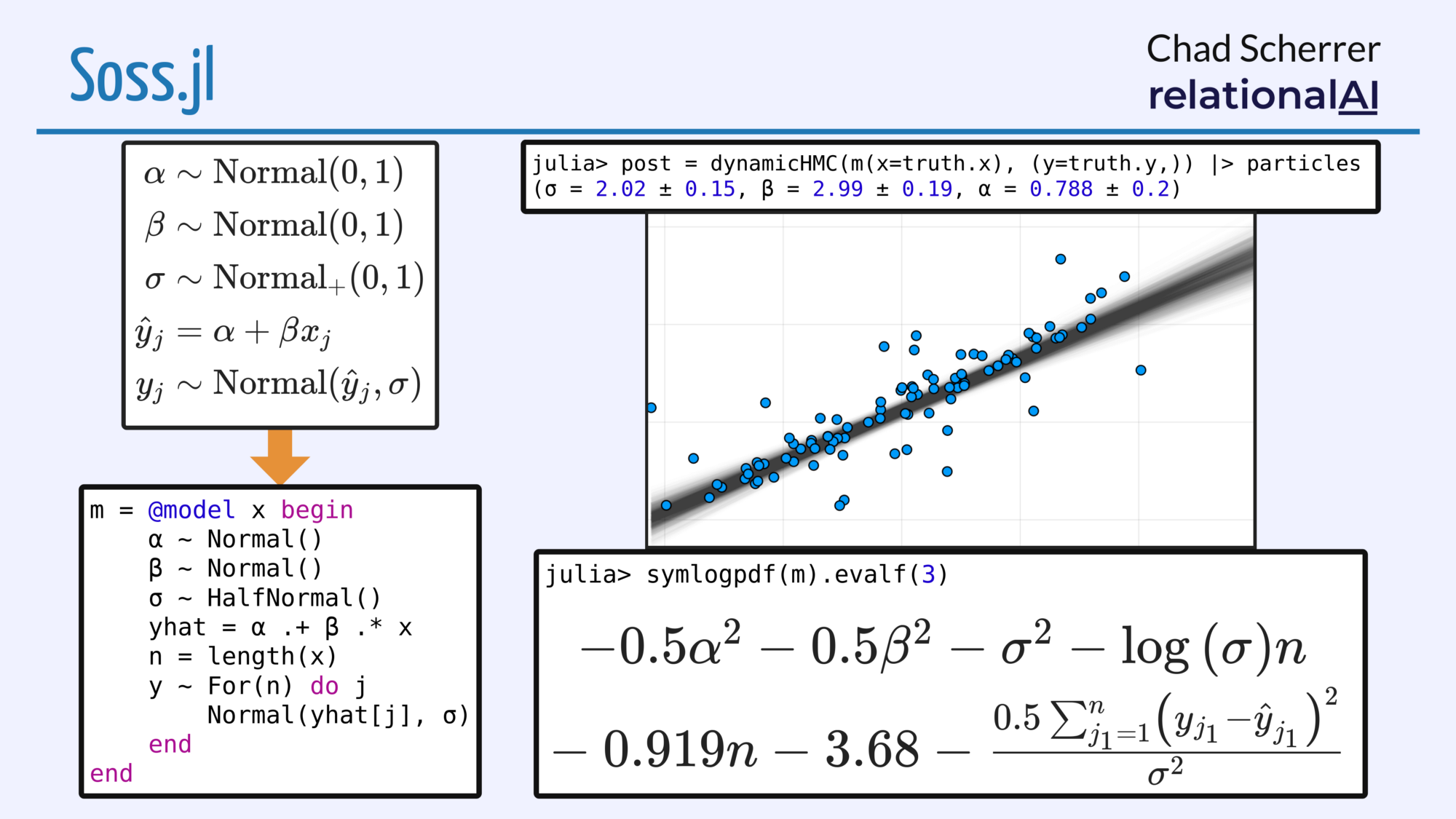
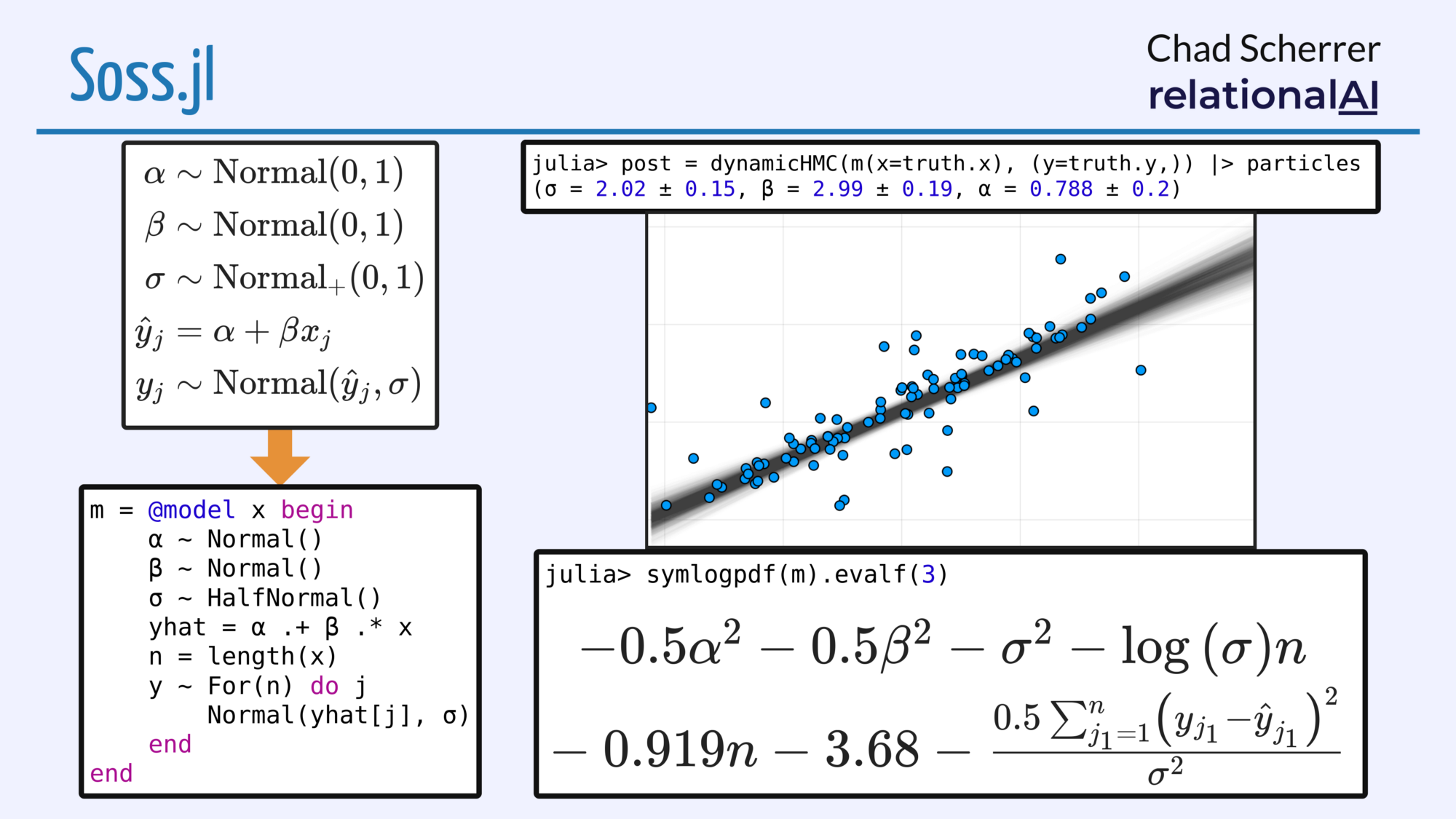
Soss is a Julia-based PPL that represents the right-hand side of each assignment (=) and sample (~) as an AST. The nice thing about this is, it gives ultimate flexibility in what a model can do. For example, we have inference methods that take a Model and return an AST that generates code at run-time, but we also have model transformation functions that return another model. Models are first-class, and can be used inside other models, etc.

There are some other things too, for example we have an interface to SymPy so you can easily get to a symbolic representation of the log-density. Simplifications here can lead to faster code, so we also have a way to generate SSA Julia code from this. There’s still plenty more speed to be had, but I’ve seen 100x-1000x speedup with this vs a direct implementation.

I’ve wanted to build Soss for a long time, it was just a matter of finding a language with metaprogramming support that could handle the syntax I wanted, while also having the speed and a good numerically-oriented ecosystem.

How does the probabilistic programming ecosystem in Julia compare to the ones in Python/R? In particular, how does Soss compare to PyMC3?

To get speed, both Python and R have to call to other languages. I’ve spent a lot of time using PyMC3, and I really like it. But it still requires keeping in your head which lines of code are talking to Python, vs which are talking to Theano. There’s a language barrier to play across, and losing track of it tends to break things.

When you write a Soss model, it’s all Julia. You can use Julia functions freely. Even if you want to do Soss development (please do!), it’s still all Julia.

On that note, who is the end user for the library, is it mostly just used in academic settings or are there industry uses as well?

It’s certainly intended for both. One thing I like about the AST approach is that generated code can be as fast as you can make it.

What were the biggest challenges in developing probabilistic programming for a new language?

There’s always some overhead in learning a new programming language. Julia has a very Python-like syntax, so learning the basics was very fast. But metaprogramming requires different ways of thinking about things, so that took a lot of spinning up.

Macros weren’t enough, we had to use Julia’s @generated functions, which let you do staged programming. Even with this, the types weren’t quite working out, so I was using eval all over the place, which does evaluation in global scope and can cause some problems.

Taine Zhao got us out of the rut with some great Julia packages like GeneralizedGenerated.jl. Generated functions compile new code for each new type they’re evaluated on, so she realized the model’s type could contain a representation of the entire model. It’s a clever solution, and helped a lot of other parts of the design to fall into place.

There seems to be an explosion in probabilistic programming on Julia with other libraries like Turing or Gen, how does Soss compare to them?

I’d say the syntax is closer to Turing, but the semantics are closer to Gen.

The Gen team independently came up with the same approach we’re using of representing a model as a function. In most PPLs, the model includes some indication of which data will later be observed. But leaving this out until inference time makes it much easier to compose models in different ways.

Any books you recommend reading on the topic, besides the classics Statistical Rethinking and Bayesian Methods for Hackers?

Both of these are great. If you’re interested in a particular system, most of the well-funded ones have a nice collection of examples and tutorials; walking through those usually helps.

If you want a broader and deeper view, I’d suggest digging into Bayesian analysis directly. One of my favorites is David MacKay’s Information Theory, Inference, and Learning Algorithms.

What’s next for Soss?

There’s always more to do. Currently we’re starting work to make the documentation better. I think we need lots more examples, tutorials, and comparisons to other systems.

If you have any questions about Soss, the Julia Discourse or Zulip are both great. And of course, there’s always GitHub issues for the Soss repo.